The “Depth of Knowledge” scheme was developed by Dr. Norman Webb at the University of Wisconsin and is used in our primary math resource, “Bridges in Mathematics” as a basis for designing instruction and assessment.In Lower Primary, we believe that students develop a deep understanding of math via exposure and practice with the FiveStrands of Mathematical Proficiency. These components work together, are interwoven and interdependent and form the overarching framework for our daily math practice.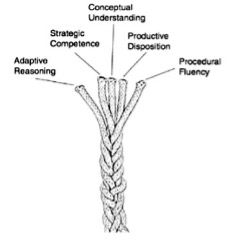 Conceptual Understanding: High achievers in mathematics understand the meaning of the operations and underlying math concepts of all areas of mathematics.Productive Disposition: High achievers in mathematics are persistent.Adaptive Reasoning: High achievers in mathematics can defend their thinking and critique the reasoning of others.Strategic Competence: High achievers in mathematics are good problem posers and problem solvers.Procedural Fluency: High achievers in mathematics can effectively, efficiently, and flexibly choose and use a variety of strategies to compute.Dr. Sandy Atkins. Parent Workshop “Creating High Achieving Math Students”. 2015The “Depth of Knowledge” scheme was developed by Dr. Norman Webb at the University of Wisconsin and is used in our primary math resource, “Bridges in Mathematics” as a basis for designing instruction and assessment.
Conceptual Understanding: High achievers in mathematics understand the meaning of the operations and underlying math concepts of all areas of mathematics.Productive Disposition: High achievers in mathematics are persistent.Adaptive Reasoning: High achievers in mathematics can defend their thinking and critique the reasoning of others.Strategic Competence: High achievers in mathematics are good problem posers and problem solvers.Procedural Fluency: High achievers in mathematics can effectively, efficiently, and flexibly choose and use a variety of strategies to compute.Dr. Sandy Atkins. Parent Workshop “Creating High Achieving Math Students”. 2015The “Depth of Knowledge” scheme was developed by Dr. Norman Webb at the University of Wisconsin and is used in our primary math resource, “Bridges in Mathematics” as a basis for designing instruction and assessment.
Five Strands of Mathematical Proficiency
 Conceptual Understanding: High achievers in mathematics understand the meaning of the operations and underlying math concepts of all areas of mathematics.Productive Disposition: High achievers in mathematics are persistent.Adaptive Reasoning: High achievers in mathematics can defend their thinking and critique the reasoning of others.Strategic Competence: High achievers in mathematics are good problem posers and problem solvers.Procedural Fluency: High achievers in mathematics can effectively, efficiently, and flexibly choose and use a variety of strategies to compute.Dr. Sandy Atkins. Parent Workshop “Creating High Achieving Math Students”. 2015The “Depth of Knowledge” scheme was developed by Dr. Norman Webb at the University of Wisconsin and is used in our primary math resource, “Bridges in Mathematics” as a basis for designing instruction and assessment.
Conceptual Understanding: High achievers in mathematics understand the meaning of the operations and underlying math concepts of all areas of mathematics.Productive Disposition: High achievers in mathematics are persistent.Adaptive Reasoning: High achievers in mathematics can defend their thinking and critique the reasoning of others.Strategic Competence: High achievers in mathematics are good problem posers and problem solvers.Procedural Fluency: High achievers in mathematics can effectively, efficiently, and flexibly choose and use a variety of strategies to compute.Dr. Sandy Atkins. Parent Workshop “Creating High Achieving Math Students”. 2015The “Depth of Knowledge” scheme was developed by Dr. Norman Webb at the University of Wisconsin and is used in our primary math resource, “Bridges in Mathematics” as a basis for designing instruction and assessment.Levels of Cognitive Demand
We want our young mathematicians to develop all strands of mathematical proficiency, to have conceptual understanding, procedural flexibility and fluency and the ability to apply math concepts in “real world” situations. In order to do this we are cognizant of the cognitive demand of tasks and strive to engage students in experiences that extend thinking.
